Kinetics

I've written a bit in the past on equilibrium expressions in chemistry, and have also noted how thermodynamics (i.e. equilibrium) is one of the two foundational concepts in all of chemistry, while kinetics is the other foundational concept. A reaction can be characterized as favorable through thermodynamic expressions, but because said reaction can take forever to take place, it can, for all intents and purposes, be considered as not taking place. This is all related to the energy diagram of a reaction:

The distance between the starting point on the left and the ending point on the right gives the change in energy of a system or species. This is the thermodynamic aspect of a reaction, and is directly related to equilibrium. The center portion, where the energy is changing in all kinds of ways, is related to the kinetics of a reaction.

Think about a trampoline. When you jump high into the air on a trampoline, it took a considerable amount of energy to get you up there (from the trampoline, from your legs). This is similar to the high points on the reaction diagram above. The molecule undergoing reaction needs to change its shape in order to become a new compound, but in order to get there it has to "jump up" into a shortly lived shape, much like jumping on a trampoline will only propel you into the air for a short amount of time. The amount of energy it takes to change a molecules shape is what slows a reaction down.

In the above diagram, we have two high points. The first high point, because of how much energy the molecule starts with, takes more energy to be put into the molecule in order to get the molecule to that energetically packed shaped. This would be termed the "slow step" of a reaction. The molecule briefly takes a more comfortable shape before having to undergo one more energetically unfavorable conformation change, and then it drops back down to the final product. However, because the molecule already has a lot of energy gained from the previous conformation, this step is much faster since it only requires a little shove to get going over the final hill.

This is the theoretical picture of a reaction, but kinetic relationships are usually represented with equations. Deriving these equations will be the topic of my next blog post.

Graduate School

I finished up the GRE this past weekend, and the preliminary results look good. After having paid for the GRE, however, the capital necessary to finance the application process is lacking. Seriously, this shit is bookoo expensive. As such, plans include:

1) Decrease the number of schools to which I'm applying. Shame, since I had researched several

2) Call the schools this week and beg them to waive the application fee

if not 2, then 3) Don't apply, but move to favorite graduate school area, take a class next year, and solicit myself in person for one year.


Option three actually doesn't look too bad from my vantage point, since having a year of not-school would likely increase my motivation going in. Not that I have major motivational problems at the moment, I just figure that it would have this effect. Option three is bad, however, in that I know I'll forget a lot of information in that year, and would be playing catch-up for the first semester rather than coming in fresh.

Seriously, how do people find the money for this? It's ridiculous that the "standard" bill shelled out (advice says to pick ~5 schools), including the GRE, is approximately 500-1000 dollars (depending on how many schools you apply to) just to hear "Yes" or "No" back from the school.

Turkey-Day, 2010

An interesting point came up at the Turkey feast today. For most of my life I've dined with the fam, which of course means that I do not drink wine, I do not use bad words, and I remain mostly quiet and polite.

However, since my family has moved away from our used-to-be-home base, I've been celebrating Thanksgiving with a close friend of mine and his wife. I bring pie over, they cook everything else. It's very kind of them.

The additional benefit to this, however, is that we're all opinionated atheists, and as such I can get drunk, swear like no other, and bray on about Socialism. In that sense, everything is actually more SOP, and thereby "filial" in the classic sense where one can expect to "be themselves and not worry about it". Honestly, I can't "be myself and not worry about it" around the family -- I know that it would hurt their feelings, and so I simply abstain. I feel no resentment for this fact, but it's still nice to find a place where you can be worry-free of what you say when you aren't exactly part of the mainstream of popular opinions.

Here's to a great Turkey day. Maybe in the future we'll forgo the turkey. Ya'know, just to make the holiday that much more sacrilegious.

Skepticon III

I just arrived back from Skepticon III to my small abode and I am exhausted. This was three days of skepticism, atheism, science, feminism, gay rights, sexuality, late night conversations, and reference-trading [I love references]. Talk about a fantastic venue. (It's also free due to the work of a lot of cool volunteers that I'd like to thank)

Perhaps my favorite aspect of these events is what seemed to be a large cross-over between the afformentioned groups: Feminism, LGBT rights, and general strong stance against right-wing religious movements. I hope these political trends continue to be introduced. It would be great to unify a sort of left-political force within the United States that aren't as blatantly not-left as the Democratic Party. Though I doubt everyone will agree with my particular politics, I'm tired of two blatantly bourgeois options.

Of those who spoke my favorite to listen to was PZ Myers. I like science things, and I thought his poker game analogy for evolution was a wonderful tool that I'm going to shamelessly steal.


Again, while this may not reach those organizers, thanks

Points of Conflict in Evolution

Last night at the Socrates Cafe (hosted by our university's Philosophy Club!) the topic was "Can religion be reconciled with evolution?" Overall it was an interesting discussion, but what I was most interested in were points of conflict between evolutionary theory and religious views. I thought I'd gather up these ideas here. From memory, it seemed there were four clear points of conflict:

A Sense of Purpose
Literal interpretations vs. Alegorical interpretations of The Bible
The relation between Man and Animal set out in The Bible.
Knowledge of man vs. Knowledge of God


Naturally this all depends on what one means by religion, what one means by God, and what a specific religion denotes. The focus was upon mainstream Christianity, though, because this is the predominant religion in our region, and therefore it is here that we were most familiar with conflict arising. I'll first explain the conflicts, then move onto possible resolutions. To explain the conflicts --

A sense of purpose: The Bible, especially in the New Testament (I'm a little sketchy on the theological backing for this statement, however) states that man is on this earth for a special purpose. This gives meaning to an individual's life as they fit into a plan of some kind that a benevolent being has orchestrated for them. The conflict arises because evolution carries a purely materialistic connotation with it -- not as a necessity, but human existence and some of its traits are explicable in material terms. More than this, we thought that the word "random chance" tends to carry the connotation that man has no purpose, and therefore no meaning within an evolutionary context.

Literal vs. Allegorical: If one takes the Biblical account of the origin of man and the universe as a literally descriptive event, then clearly evolution and The Bible conflict. According to The Bible, man was created in God's image exactly as he is now. According to evolution, he was one of many species who made it to this point.

The relation between Man and Animal: According to The Bible, Animals were set upon the earth for men to use and take care of. This places man above animal. There comes a conflict with evolution when man is taken to be an Animal, because this relation is, at least in part, dissolved.

Knowledge: Some religious traditions claim to have knowledge of a superior or different kind. Because evolution is a man-made construct that admits itself of being tentative always, and because Godly knowledge is necessarily perfect, a conflict between scientific claims and religious claims arises in that a religious individual who believes to have a superior kind of knowledge will simply dismiss evolution tout court. In addition to this, the teaching of evolution might be frowned upon as it introduces a different way of looking at the world that may influence their children away from the perfect knowledge that the believer has.


Resolutions


Purpose: This one is complex to resolve because it is highly dependent upon how one interprets evolution and how one interprets their religion at a metaphysical level. However, one clear resolution seemed to be pointing out the meaning of the word "Random". Random can be easily confused because it has several meanings, and in the context of biology it has a specific meaning that probably doesn't reflect what one would consider "Truly Random". In the context of biological evolution, randomness isn't necessarily stochastic so much as it is unpredictable. An example may help here:

Mutations to genes can be introduced by a number of inputs. An example of a random input would be the molecular machinery making a mistake in transcribing DNA into RNA. Instead of the base that the machinery is supposed to pass along, another is put into place. This piece of RNA will then express another amino acid, which can change the function of the protein which is being made. This change of function almost always leads to a decrease in an organisms function -- it is unable to reproduce, whether it be because of death or some other reason. However, it is possible for this mutation to make a positive contribution to an organisms function, in that it is better able to reproduce than its fellow creatures. In either direction, this is a "Random" mutation. It may not be "Truly Random", but this is what the term is meant to imply -- that some changes are able to be accounted for, but are not predictable at the level of predictability that one tends to expect in a scientific theory. As such, evolution isn't "Random" in the sense that we don't have a purpose. I used the term function on purpose. There is an interesting analogue here.

When Adam and Eve leave the Garden their purpose becomes to have a family. In a sense, this is their function. They must plow the earth and work in order to procreate and be happy. Similarly in biology an organisms fitness can be simplified to their ability to procreate. The function of life is to create more life. If one doesn't take the Bible too literally, the parallels between these supposedly disparate disciplines are interesting, which leads me into the next resolution.


Literal vs. Allegorical: A literal interpretation is clearly irreconcilable with evolution. I won't get into whether a literal or an allegorical interpretation is better, but I will note that allegorical interpretations are in almost all cases reconcilable with evolution.

Some interesting parallels exist between the creation story of the Bible and currently accepted scientific cosmology. While God separated the light from the darkness, the current model on the universe's beginning is the Big Bang. The Big Bang doesn't explain the question of being in the least, but it does start with a large conflagration where all being was mixed. With time the light was parsed from space. In the second creation story within Genesis there is a parallel between what is created on Earth and what currently cosmological models describe. First came the waters, then came the plants, then came the animals, and then came man. The Knowledge of Good and Evil corresponds to man's birth of consciousness. The innocence of species-hood without higher cognitive functions was a sort of bliss. A new perceptive ability brought about the realization of pain in this world, work for our bread, and a longing for a heavenly existence. I didn't come up with that story, but I think it's neat.


Between Man and Animal: This is something of a specific problem, since not everyone will think that their religious background gives them right over animals. However, supposing that man is greater than animals -- If one accepts the doctrine that man is fallen, then there shouldn't be a problem in accepting that Man is an animal. Man can still be greater than other animals, in that he prefers those rationally inclined, but it seems to run parallel with theological teachings to assume that we actually have an animality. In Christianity this animality is to be overcome, something which I can't say I agree with, but the existence of animality seems to go with, not against, religion.


Knowledge of Man vs Knowledge of God: Here I don't think there is a resolution. I only think it important to point out that in "Knowledge of Man" (i.e. Science) class that we should stick to the subject matter of "Knowledge of Man". I have some theological problems with revealed knowledge, but that is outside the scope of this post. Still, it seems unreasonable to be worried about knowledge of man infecting a child's knowledge of God if the knowledge of God is perfect. There shouldn't be much worry at all here.

Evolution, Science, and Politics

Tonight I saw a film at my university titled Kansas vs. Darwin, with the filmmaker present, Q&A session, dinner, the works. It was very nice. While I've always maintained a certain fascination with Creationism, et al., I wasn't quite aware to how widespread beliefs in Creationism are. After watching the film, I decided to investigate what Gallup had to say:

2004 Gallup Poll on Americans beliefs: link
2007 Gallup Poll, coupled with some healthy Republican bashing, which reveals a similar trend: link


Now, I'm no social scientist, so I wouldn't say that I have the theoretical backing to interpret this data as well as it could be. But the trend is strong, in that Approximately 1/2 of Americans believe that God created man in his present form. This lies in contradistinction to the 1/3 of Americans which reject Evolution as a theory. I think this disparity is explainable in light of creationist beliefs that there is a difference between micro and macro evolution.

The percentage numbers on this are staggering, however. I'm from Kansas, and so from the filter of popular culture, news, as well as some personal experience (organically flavored with personal bias) I knew that there existed quite a few individuals who rejected the theory of evolution. From reading creationist websites, however, I gained the impression that this was a fairly fringe group of individuals due to the nature of the claims, and that I just so happened to be lucky enough to live in a blood-Red state, where bouts of insanity are viewed as acceptable (I'm more joking than serious). Clearly, however, these suppositions are wrong. The shear percentage of individuals refutes my supposition that "Creation Science" is a fringe movement, politically speaking, and the film above stated there was... somewhere around 27 other states going through similar struggles? I can't remember the exact number, but it was greater than Kansas + Texas, the two likely candidates.

From the dinner and the video viewing, it seemed that this widespread belief could be explained on the basis of what possible philosophical implications the theory of evolution entails. There is certainly a movement of persons who believe that the theory of evolution entails materialism, atheism, a loss of moral value, and/or the loss of human dignity and specialness. I am not of this group of individuals.

However, it seems that there is this perception, and it may best be explained by two notions: The notion that Animals are inferior to Humans, and the notion that God created Man in his own image.

If man is an animal, then the inference from evolution is that man is not special. This contradicts our notion that man is a special being with a special purpose above that of the animals. Therefore, evolution must be wrong, because it animalizes man. On the face, outside of arguments for evolution, this is a convincing argument -- one may look at animals in the zoo and conclude that there is a world of difference between us, and because we value ratio-emotional-linguistic expressions that happen to communicate well with us, one may conclude that man is a special sort of creature above the animals. This explains the large number, at least in part.

The second notion: If man was generated by natural processes, then he was not always in the shape that he currently is in, and this contradicts Biblical teaching. If Biblical teaching, supposedly incontrovertible, is wrong in one instance, and The Bible must be taken as a literal whole, and The Bible is the basis for moral beliefs, then the theory of evolution threatens not only the historical myths upon which moral beliefs are found, but the moral beliefs themselves.


It seems to me that, for the regular individual involved, they aren't interested in scientific truth. The individuals involved are interested in a spiritual truth. However, on top of this layer of worry about materialism and the decay of moral values in a Godless society predicated upon natural selection there seems to be a strong political current. The 2007 Gallup Poll suggests that Republicans are catering to this sort of audience. This is pretty much standard fare tactics for the Republican party (promising empty metaphysical maybes to convince rural districts to vote against their economic advantage), so I wouldn't be surprised if a large section of this percentage is explicable in terms of political clout. Something else mentioned at the film was the divisiveness of the topic of evolution, and the fact that those against evolution bond together socially over their non-belief in evolution. It would seem plausible, given the Gallup poll above, that the Republican party is cashing in politically on this movement, which would explain why it is widespread -- it would certainly explain where funding for the institutions which pump out creationist literature come from.

To ask these social bonds to be dissolved is to ask too much. But, simultaneously, to ask people to believe in the strongest scientific conclusions within a Western society isn't asking very much. This hints at another source of the problem: Science Education being horrible, and science education being horrible not just because we live in an anti-intellectual culture that values funding imperialistic ventures for its stockholders (though that doesn't help). There is a disconnect between the scientific communities expectations of scientific literacy, and their willingness to put effort into educating the public on scientific matters. This is natural, given that careers are built on publications and patents (which, coincidentally, happen to be the things which support the Market). But if the scientific community wants the public to be educated, and given that the public funds the scientific community they honestly have a right to know what's going on, they need to change their attitude towards outreach programs and the value of popular science work. If these become worthwhile career enhancers (though that shouldn't be the bottom line in choosing who popularizes and who doesn't) then we're likely to see a rise in scientific literacy.

ACS Conference

My poster was admitted to the regional ACS conference this coming October! Results are pending on a single experiment (it was done once, but the data was difficult to interpret so we're subbing some expensive taq for the not-as-expensive taq we used initially), but they looked promising from the first run. Either way, my undergraduate research requirement will be satisfied, and if the results are positive then they should be publishable.

Which brings me to a point I often question about the scientific process: Why don't negative results get publishing, at least, more often? I'm assuming that it's more of a principle of parsimony in publishing than a fascination with positive results, but sometimes I wonder... is there a database where one could at least throw up negative results? Maybe it wouldn't count as publishing, but something like this would be great because... well, it could potentially stop other research groups from traveling down the same avenue, thereby limiting the amount of resources wasted on the same question. This, at least on its face, sounds like a good thing.

Some Possible phil-o-sci Problems I want to solve

How do you properly disseminate scientific information?

Problem 1: The expert, and consensus. Consensus can be achieved amongst the respected scientific community on controversial (whether that controverys be manufactured or no) issues. The obvious topics here are evolution and global warming. However, the problem isn't with the scientific community achieving consensus. The problem is disseminating that consensus, and determining when one can claim scientific consensus such that it is acceptable to use this term in popular discourse. I take it at face value in this blog post that both evolution and global warming are issues upon which consensus is reached. The problem here isn't with the science; it's with our vision of the expert. A society unequipped with the rational equipment to distinguish between good and bad scientific claims -- and not in an immediate way. The research can take time -- is exactly the sort of society one would expect to see if it that society relied upon the image of the expert. The problem of the expert isn't that experts shouldn't speak; quite the contrary. The problem is that theatrical devices can achieve the image of the expert without the substantial mental effort necessary to become an expert. Additionally, the problem of the expert lies in the fact that experts will disagree, yet we lowly types not in the public sphere still need to be able to distinguish which expert is the better expert. This is particularly relevant in issues of basic scientific theory which happen to apply to political issues; because one can find a person with credentials who is willing to adopt a viewpoint, and use their expert status to back it up, we have a culture wherein we can easily select for the expert that happens to make us feel comfortable with our viewpoint. This is confirmation bias at work.

I state the problem of the expert because it is my opinion that this is a more basic question in the philosophy of science than the problem of demarcation. All solutions for demarcation have, at present, only excluded things which most individuals who have chosen rationality already excluded for basic, philosophic reasons. The problem of demarcation is, itself, a problem. If, instead, the philosophy of science concentrated on generating thought-technology for the lay man to integrate scientific knowledge, and to do so without excluding the majority of viewpoints already held dear, then the problem of demarcation would be swept away as an interesting question, in the same way that the problem of being is an interesting question in metaphysics. The problem of consensus is something of an ejaculatory beginning to a question I have that may or may not produce anything -- it may just be an intellectual curiosity. But it seems that one should at least have an idea when consensus is obtained if one wishes to integrate scientific knowledge into a population that, itself, does not practice science, and may not be interested in science enough to be educated in science.

Problem 2: What to integrate? As I'm heavily influenced by Dewey in my educational philosophy, I am interested in teaching methods to knowledge. In the context of science the problem with this is that science doesn't have a method, or rather that the method itself is also constantly evolving and changing with what is judged good by those practicing science, and is better learned by doing science than by formalization, but simultaneously one needs to "catch-up" with the facts before this process can begin. This is a necessity for the progress of science, but it does leave one contemplating the educational question in a quandary: What do you teach the public? Just the facts? But the facts change. The method? Again, so does this. That which is relevant to policy decisions? But here we run into the problem of the expert, and setting ourselves up as experts, which appears, in a theatrical sense, exactly like any expert. (Relevant side note: this highlights just how important Aesthetics are, or can be)

Problem 3: Alienation. While the wonders of science are wonderful to those in the in, the wonders of science appear mechanistic and destructive to a large fraction of the population. And this isn't totally unfounded -- the scientific community should never play apologist to the atom bomb, for example. I think it is in the problem of alienation that one is best able to explain the reaction against evolution, for example. Our cultural understanding of spatio-temporal explanations fall on the logical side of the divide, while our values fall on the extra-scientific side. And, what's more, the scientific community doesn't actually question itself on questions of the ethical impact of disseminating scientific knowledge. Scientific knowledge needs be known -- the end. While I'm sympathetic to the need to disseminate knowledge, we also need to question How it is disseminated, and in what way it ought to be disseminated. Several viewpoints which seem to be working great for a large section of the population on their quest towards happiness (the real point of life) run counter to scientific knowledge. As Bertrand Russell said in What I Believe, you need knowledge in addition to love. The problem of alienation arises through our pursuit of the first and our negligence of the second. An answer to this question of alienation is the active integration of scientific viewpoints with existing, followed, and practiced philosophies that seem to work and don't run counter to being able to participate within this rational process. The ethic of this type of work should be -- if a worldview can be justified, then it should be justified. As I've become accustomed to a virtue-theory ethic, this can be justified by our cultural value of pluralism.

An epistemic reason for religious tolerance

Yesterday evening just before I left campus I received a phone call from the local LDS representative assigned to myself by the church. My father always forwards my address when I move because he cares about my eternal salvation. It makes sense when you consider his perspective, and usually I don't really mind the occasional visit from those who love God because I find the conversations fun. However, last night was not the best night for myself. I tried to intimate that, but he offered tonight, so I was all "Yeah, sure, come over, whatever" Being somewhat on edge due to a busy schedule, and not really feeling like putting up with the fellow, I decided to pour myself a double before he came over. Unlike other times when he'd come over to share the word, where I would attempt to politely but firmly point out my objections, I was not quite so polite this time around. There's a sense in which I feel bad about this, 'cause the guy's an old retired man, and really, of all the times in a person's life this might be the worst time to start edging in on their religion, God, and all that. They lived the life, they might as well receive some sort of comfort compensation when coming near the end of it. So, hey, I can't say I'm proud of it. But I did come up with an interesting insight from the conversation none-the-less (This is probably the least inflammatory comment, which just goes to show me that polemics are better comedy than philosophy).

Of those religions that I am familiar with, and seem to be wildly popular (Christianity, Judaism, Islam), all of them claim that God is in some way infinite. There are interesting philosophical developments in the understanding and concept of God, and some theologians come-with, but when approaching the usual basics of these religions (and I fully admit here that I'm at a loss when it comes to "Eastern" traditions), and the beliefs of what seems to be canon to these religions, God possesses infinite properties (to some, within the scopes of logic, to others, not so, and so much the worse for logic).


Additionally, from what I have seen within these religions, it seems that man's finitude, at the least as a moral being, is central to their system of understanding the world. Yet, despite this finitude, these religions will often have claims wherein this religion is the true religion amongst religions. While this is a common objection amongst non-believers (adopting, at least temporarily, intersubjective agreement as truth), what I did not realize before was the contrast between the infinitude of God, the finitude of man, and how this directly contradicts any religion's claim to the one true path to God. It is not that, granting God, we can't understand a segment of God or experience the divine. It's that many people make this claim of perfect or nearer-perfect knowledge of God, and yet the doctrine of God's infinitude and man's finitude necessarily leads one to conclude that man can't understand God, as he can't understand the infinite. As such, one ought to conclude that one's religion is but a path to the divine, something that a given individual thinks is correct, but is itself not the best, or at the very least possibly not the best, description of God and his will. To think so is to adopt a religious chauvinism that abuses God for one's religion when one is supposed to instead revere him; clearly, a contradiction. It is for this reason that we should reject faiths that proclaim themselves True.

Ontology and Science

Last I blogged I mentioned that building an ontology on top of scientific models currently strikes me as a bad idea. Here's why.

A rough outline of what ontology is is the study or question of that which exists. It includes exploring the meaning of "Being", "Essence", and questions such as "How can anything exist at all?", "How do you know if something exists?", the existence of God, or universal laws, or questions which reflect upon the meaning and nature of time and matter. I wrote this in order of seeming increasing relevance to scientific questions to give the impression as to why it is one might seek the answers to the questions of ontology in scientific investigations. Surely, scientific investigations use concepts of matter, time, natural law, and attempts to elucidate the mechanism and relation between all that is posited as is to give a cohesive picture of existence. There is an attendant epistemology, and supposedly, there isn't a reference to ethics outside of the confines of this epistemology (things like "Don't fake data", etc.)

What is posited as is, in science, is posited as is not on the basis of asking what is, but on the basis
of asking a general research question. This research question is formulated on the information already present from previous generations scientific careers. The information generated previously was generated not to find what is (usually), but to also answer questions that seemed relevant on the basis of what was passed onto that scientific generation. In short, science progresses towards seemingly relevant research questions generated upon data that was generated on previous research questions. This process can be directed towards other things than asking what is, especially given that one's career depends upon their publications, and the citations to these publications. This process of information generation seems to be predominantly directed towards economic benefit for those who are able to invest, military applications, and the health of those who are able to afford care. So, the process of science, current science, whilst I won't deny the position of scientific realism, isn't trying to answer questions one would prima facie think belongs to a scientific realist's set of questions -- instead, a good demarcating point for scientific knowledge is the knowledge which assists in humanities power over nature, and due to our economic situation, this power of humanity over nature becomes the power of the rich over that which isn't rich.

I will note that this isn't a necessary evil. It just makes science non-ontological, at least in the sense where one attempts to answer ontological questions primarily. Since science doesn't usually answer ontological questions, it follows from this that referencing science in answering ontological questions can be faultier than one might first assume.

Another good reason to not mix these two disciplines is that if one were to mix ontological questions with the scientific enterprise, the scientific enterprise would likely come to a halt -- if one runs a quick probability calculus on the history of ontological questions, one could easily conclude that it is highly probable that ontological questions are insoluble. Based upon this, we wouldn't even want to build an ontology on science for the fear that science wouldn't operate, at least if it is the case that we want science to operate as most people who build ontology on science do. Instead, science assumes an ontology (A formal, universal ontology based in the concept of "energy", and thereby an ill-defined sort of physicalism, upon which general principles of other disciplines that are supposedly "smaller" are loosely attached to), and then gets to work attempting to describe the universe with that ontology, as well as with a ever-morphing epistemology. I can't stress enough that these are good things for the scientific enterprise, so long as the scientific enterprise continues to value producing knowledge which generates support from governments and industry.

Approaching science from the questions of ontology, one realizes that science isn't the "objective" viewpoint that ontology looks for, as is often thought. It's an approach to ontological questions that tends to beg the ontological questions with a rough rational-empirical epistemology of some kind (and even this varies with the discipline, the scientist, and with history). If one is not a scientist but wishes to build a scientific ontology, then one will often employ a half-hearted Popper reference. Science seems to operate underneath a value-set, in the same way that Popper's Scientific Logic operates underneath a value-set, and proclaims this value-set as a methodology to mask the fact that it is, indeed, a value-set. Now, I have no problem with mixing my epistemology with my values -- but I'll mention that my value-set doesn't include falsifiability, numerical accuracy, and prediction-of-outcomes as prime. There likely somewhere down the line, but my prime values include compassion and equality far before what experimental parameters supposedly require, and it would do so whether or not the current psychological theory proclaimed that this should be so.

This leads into my final point on why I, on a personal level, have stopped attempting to build an ontology on top of science: politics. While this process is more self-correcting in my view, the scientific enterprise would mirror some religious power structures in an uncomfortable way the moment that science starts proclaiming ontological truth to individuals not trained in the abstract difficulties of scientific knowledge. It seems to me that a better approach is to relegate science as an epistemic approach to solving abstract puzzles related to power-over-nature, an end that is valuable unto itself, but not valuable as ontological constructs -- at least, not as ontological constructs to anyone outside of the scientific community. If one is able to retort to a scientific argument, then I don't have a political problem with a scientific approach to ontological questions. However (and note that this is with good reason -- the problem isn't with the scientific enterprise, only with mixing science and ontology) the majority of the population can't reject scientific claims because they lack the background. Any structure that can proclaim uncriticized truth (to those who aren't in the community) is just asking to become a political structure. This would likely destroy the scientific enterprise.

Seeing as I don't want science to become a political entity, and seeing that both ontology and science seem to mutually destruct one another, it seems wise to me to perhaps allow each to inform the other, but to keep them separate in some sense... I'm not sure exactly how to succeed in doing that, however. Science jumps out as a source of answers to some pretty basic ontological questions, and it answers these in a pretty successful manner. I just don't think importing this ontology to ontology, or other areas of life, academic and otherwise, seems to be pertinent at all -- science doesn't have a general epistemic approach (unless one wishes to interpret it teleologically), and it really only deals with pre-defined description problems that themselves are highly oriented towards control over nature. Honestly, this has about zilch to do with what's important in life, excepting the fact that scientific exploration is interesting unto itself for some people and therefore important to some lives.

After summer thoughts on Science

*cough, cough, bleh, blewy* I have been resurrected! Indeed, the summer was full of research fun and things very un-blog-related. But now, a few weeks into the semester, I return to my little patch of the internet to update.

And, with that in mind, I've recently come to the realization that I've forgotten a lot of science. Over the summer I focused in on a single research project, and became very good at the processes' that guided that project. I'm still a little fuzzy on the details (i.e., I need to run a few more experiments to get some results), but overall I'm confident I understand this little piece of science that I can call my own. However, as I return for my senior year as a chemistry major, I'm sort of blown away by what, of the general theoretical chemical understanding, I have to remind myself of. There is a sense in which I've integrated a large number of facts into a process, but it still kind of freaks me out. I'm certain that, were I more dedicated to the sciences, and cared less for things like literature, philosophy, theatre, and all the varied "unrelated" disciplines which constitute my hobbies, that I wouldn't need reminding. I would have reminded myself through biographies, pop-sci publications, and so on. In short, if I cared more about science I'd be a better scientist. But I don't care so much about science that I want to dedicate my whole being to it. It's an interest amongst interests, and it happens to be better funded both academically and industrially, so I pursue it.

After this summer I've begun to think that science (at least of the physical variety) is just fun- there are more important things in the world than it. And I'm more hesitant of basing an ontology on scientific pronouncements. Lastly, I've come to think that the theory of evolution is probably the strongest scientific theory, which is counter-intuitive to the usual "Heirarchy of the Sciences!" I may just write an essay on it, if I get around to it.

I think all these altered thoughts on science came from actually doing the research itself. Somehow, in the process of learning the models of physical science, the education itself seems to lull one -- sure the models are good, and the training rigorous, but the models are set. There isn't as much "critique" as one might think, at least at the undergraduate level. Having some experience in this, now, it's hit me how much of science is. . . made up? At least in praxis. Not that this is a bad thing. I've always defended art. It's just struck me how much science, while awesome, beautiful, and fun, really isn't the holy grail of epistemology like I thought. It's an approach amongst approaches, and a rather nice one at that. But I'm hesitant, now, to place it even at the top of the epistemological food chain. It's robust, but not superior. It's good, but not the best. It's worthwhile, but not to a singular point. I think that expresses what I mean fairly well, without getting into the nitty-gritty of an argument (something which, at the moment, I'm still formulating to be honest. But I know I've hit upon something here. It's just. . . wider and more disjointed than what this blog post can express)

Process: Work

The first law is concerned with the internal energy change of a system. This is what ΔU represents. As I admitted earlier U is an odd concept to me. I think this primarily arises because, at least chemically speaking, we're mostly interested in the changes in U. Changes in energy I am comfortable with, and the way in which they change is what the right hand side of the equation describes: namely, q and W. These two symbols designate every process that could possibly change the internal energy of a given system.

"W" stands for work. Work can encompass a large number of things. Work, mechanically speaking, is defined as
In a mathematical context, and in one dimension. This simply states that a Force (From Newton's 2nd Law F = ma) applied over a distance equals the amount of work done. If you happen to be unfamiliar with integration, the long squiggly sign is the mathematical way of saying "from point A to point B", and "dx" means the change in position x (like a Cartesian grid, such as you learn about in algebra class). Work can come from more than mechanics, though: It can be performed by electric circuits, or chemical reactions (cell phones, vehicles), or some other type. In the end, however, it's still work.

Thermodynamics is largely used to describe gas phase systems. This doesn't have to be the case, but the gas phase is effected by thermodynamics more so than solid and liquid phases, at least with respect to the phases we normally encounter. As such, work is not defined in the mechanical sense. Instead the concepts of pressure, volume, and temperature are used, and work is defined as
Where P is Pressure and dV is the change in volume. The reason for the negative sign, in this context, is a matter of definition. When "negative" work is performed, this indicates that the system of interest (in this case, a gas) is loosing energy (or releasing energy, as an equivalent expression) to the surroundings. If the integration produces a positive sign (by having a negative PV), then this indicates that energy is entering the system. This is actually analogous to the above definition as mechanical work almost always gives energy to the system: A force applied to a ball from point a to point b will give energy to that ball. But in the context of gas description the application of a force would decrease the volume of a system, which mathematically would give a negative "PV", which goes against the convention of negative = release energy from system, and positive = give energy to system.

Looking at this, the "process" part doesn't seem to be coming into play at all. If you go from point A to point B, won't the distance between these points be the same regardless? As stated so far, it seems that way, but there's one other aspect of integration that works into the idea of "Process" here. An equivelent way to look at integration is that it gives you the area underneath a curve on a Cartesian grid. For example, this:

would integrate to give the area of the black shaded block here:
As such, integrating a function like this:


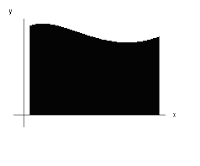
Would give a much larger area in comparison to the first one, as can be seen here:Sorry for the math digression, but I think it's important to understanding the concept of processes. When I took Chem I, the whole "you can go different ways to the top of a mountain" shpeal only served to confuse me further.

The great thing is there is such a function that describes gases and relates to our function for work. It is known as the ideal gas law: PV = nRT. In most thermodynamic cases, n is constant (and stands for the number of particles), and in all cases, R is constant (Specifically, named "The Gas Constant). Rearranging this algebraically gives
Which states that P is a function of T and V, or P(T, V). We can plot this in three dimensions, but there's no need: If you have two of the numbers from above, whether it be pressure, temperature, or volume, then you can find the third as n and R are held constant. Also, since we're interested in work, we might as well label one axis and pressure and the other as volume since those are the two variables that determine work. I'm not sure why this is the case, but I've never seen it otherwise, so I'll state that "By convention" the x axis is volume, and the y axis is pressure, thereby giving

Now, analogously to the Cartesian plane of algebra, every point on here is defined by some number, but here the number has a unit, or a meaning, attached to it: Namely, the pressure or the volume associated. Also analogously to the Cartesian plane above, if you "integrate" from one point to another on this plane, you will obtain the area associated with it. If you recall, integration from "Point A to Point B" [Or, rather, from point (Vo, Po) to point (V, P)] was also the definition of work. In other words, the area of a block you would obtain by moving from one point on the plane to another is equal to the amount of work performed. The actual path that one takes is the process one uses to get from one point on this plane to another. Therefore, the process described by this path:

Takes (or releases, depending on which point you start with) less energy than this path:



That is why work depends upon the process taken: Because it is the area underneath the curve which would be drawn from one point on the Cartesian Plane of Pressure-Volume to another point. If you were to decrease pressure and then increase volume, you'd be doing less work. If you instead increased pressure before increasing volume, you'd be doing more work.

Each of these paths have special names attached to them that designate what's happening. The first PV-integration example is called "isothermal", meaning that temperature does not change in the process, and the second is "isobaric" meaning that pressure does not change in the process. Some other processes I can think of are "isochoric", which means that volume is held constant (No work done), and "adiabatic" which means that energy is not lost or gained through the other process involved in determining the change in internal energy: Heat (q). I'd go into heat, but I think this one is long enough as it is, so I'll reserve that for next time around.

Penny Experiment, trial 1

When I was in middle/high school (I don't remember which) we dropped pennies into sulfuric acid to watch them react. I remembered this to be a lot of fun, and at the beginning of this semester I thought I'd try an "at-home" version with vinegar to see if dilute acetic acid would do the same thing. I expected it to, as hydronium should still be present in solution, but I expected the kinetic to be severely limited since there wouldn't be as much hydronium in solution.

So, run 1: I filled a ceramic coffee mug with "5% acidity" vinegar, and placed a penny (post 1984) into the acid and let it sit. Two months or so later (I probably should have documented this more rigorously, but it was just a curiosity on my part), water had evaporated but the penny appeared to be identical aside from some black grime (whatever that grime is made of) that was more easily removed. So, I had a shiny penny.

Run 2: I'm trying to stick with the "easily in reach within your home" type chemicals for pop-experimental purposes. It was suggested to me that I add salt in order to form a little HCl in solution. Seeing as the other experiment didn't work at all I thought why not, give it a try and see what happens.

I filled the coffee cup with fresh vinegar, and then poured salt to fill the coffee cup ~ 1/2 way. This would ensure a saturated solution of salt in vinegar, thereby possibly driving the reaction to form HCl. Then I dropped the same penny in. ~ 2 weeks after I started the experiment, I noticed that some dark splotches were forming on the salt. When I pulled the penny out to examine it, I thought I saw some zinc, but I wasn't positive if it was just me looking for it, so I through the penny back in. Just today (some odd 2 weeks after the last check) I pulled the penny out and sure enough: holes had been eaten through the copper, and some of the copper surrounding the holes was easily removed as the zinc underneath had been oxidized.

Very neat! The salt certainly sped up the reaction (though I'm not sure if it's acting as a catalyst), from my rough qualitative memory watching an at-home experiment when the fancy strikes me. There was also a pretty cool crystal layer that had formed as the vinegar had evaporated again. I think the evaporation likely helps in reacting with the penny, as the concentration of acid is increasing as water evaporates. I'm somewhat curious about the composition of the crystals (Sodium acetate? Sodium Chloride? Sodium Iodide, as it was iodized salt?). The primary thing that's mystifying me at the moment is: Why did the salt actually help in this reaction? HCl, being a strong acid, would dissociate completely, and so would likely not form to an appreciable amount -- I would expect this to hold even in a saturated solution of NaCl. If anything, I would think that the ionic atmosphere would play a larger role in interfering with the equilibrium. Of course, I also used the same penny after the last one, so I'm thinking I need to redo all this with a new penny at least. And, so that I don't have to use a pH meter (or titration... but for this I'd likely deal with the error in the meter) to find how much hydronium I have at the end, I'm going to try covering the coffee mug so that no water evaporates. Still, kind of some interesting preliminary results.

Thermodynamics: The Uno Law

Beyond the basic chemical equilibrium context, to understand Gibbs free energy you need to understand thermodynamics in a "ground up" fashion. The thing is, I'm not sure even I understand thermodynamics in a ground up fashion. This was part of my motivation to start blogging on it: To keep me thinking about the concepts such that they might eventually click.

The thermodynamic approach I was taught started with quantum mechanics, moved into statistical mechanics, and ended on thermodynamics. What's nice, from a chemist's perspective, about this approach is that the quantum model of the atom elucidates a lot of qualitative understanding of the atom you pick up in earlier courses, such as bond strengths, aromaticity, and IR spectra (or spectroscopy in general). Then statistical mechanics utilizes the energy levels found in quantum mechanics to make macroscopic predictions from the quantum model through statistics (ergo: statistical mechanics).

However, when approaching thermodynamics, then, outside of the basic chemical approach linked to equilibrium, I found the study to be very odd. I have been acquainted with explaining macroscopic observations through microscopic models, so it was hard to think "Macroscopically", even though the mathematics was simpler. So, in approaching general thermodynamics I think it's important to remember what it is thermodynamics is trying to describe, as that is where I lost a conceptual foot-hold in the race (and resorted to math to get me through, as opposed to understanding the concept behind the math)


Literally, thermodynamics is describing the movement of heat. But more is involved than heat: there is also work. So the name isn't exactly the best. What helped me was in emphasizing the macroscopic nature of thermodynamics. It models a large system of particles within some kind of surrounding environment. We are free to define the system, so the system is chosen such that something interesting can be measured or for conveniences sake.



In this case, the system is a beaker with a piston. The little green dots are supposed to be particles of gas floating around inside the beaker. The system stops where the beaker begins, and the surroundings begin just after the system stops. This allows measurements of the gaseous behavior alone to be recorded.

Thermodynamically speaking, there are three quantities that define this system: Pressure, Temperature, and Volume. Of these three, you only need know two to know the third as they are related through the ideal gas law. (Note: There are more "equations of state", as they are called, than the ideal gas law. But it's the simplest and gets the point across)

However, the ideal gas law isn't enough. That just defines the "State" of the system. It doesn't tell us very much about how much energy is transferred from or to the system in going from one state to another. And that, I think, is the best way to think about thermodynamics: the amount of energy transferred in moving from one state to another in a macroscopic system. Macroscopic states can be defined by the three variables of P, V, and T, and the movement between these states requires energy to enter or leave the system. How much energy enters or leaves depends upon the way in which one moves from one state to another.

That leads to the first law of thermodynamics. There are many ways of stating this law, but when trying to understanding how much energy passes into or out of a system due to a process the following is used:

ΔU = W + q

Where "U" is the "Internal Energy", W is work, and q is heat. Internal energy, to me, is a weird concept. It's this energy that's.... there?... inside the system 'n stuff? Yes. That's exactly it. Personally, I'm still wrapping my head around the concept -- the best I can do is to say that it represents every shred of energy that is within the system, from the vibration of bonds, the momentum of molecules, the mass of the atoms, the potentials of fields, EVERY source of energy that happens to be within the system. That.... I think is it. And, frankly, we don't even care about the total internal energy, but rather the changes in internal energy, because those are much easier to measure than absolute internal energies. (ergo: Δ)

So, changes occur in internal energy, and those changes are equal to work and heat. These are the processes by which energy is removed from or added to a system. They both transfer energy, but they do so in different ways. For now it is enough to understand that the changes in internal energy occur through the two processes (or mechanism, or "How-to", if that makes more sense?) of work and heat. What those processes encompass I'll blog about later.

Free Energy

A point I found difficult in studying thermodynamics as a chemist is that the concept of Free Energy is much more important to chemical study -- but it is a more deeply derived concept based upon thermodynamics and energy transfer in general. I often try and think of ways to build a conceptual framework within chemistry without referencing the physics that it is based upon, because in the end, the physics isn't totally necessary for gaining an understanding of the chemical picture. This is why I began blogging this month from the "end-point" of thermodynamics with respect to chemistry: Equilibrium. If you can understand equilibrium in general, then one should be able to understand chemical equilibrium. And, hopefully from this, one should be able to understand Free Energy.

In the previous two posts I attempted to explicate equilibrium as a general model and as a model for chemical systems. This works if you think about atoms as "billiard balls" connected to one another through "Bonds". When a chemical reaction occurs, the bonds in the reactants are broken and the bonds in the products are formed through some kind of process. To deduce an equilibrium expression the step-by-step process does not necessarily need to be known: All that need be known are the ending concentrations of the products and the reactants. The reason that these concentrations are constant is not that the chemicals stop moving due to some mystical equilibrium constant that brings out the golden tablet of concentration stating "Thou shalt not react!" Instead, the chemical species continue to react both in the forward direction (Towards products) and the backward direction (from products to reactants), it is just that at equilibrium these processes occur at the same rate. What those rates are is another story -- but what those concentrations are when the rates are equal is driven by Free Energy.

Free Energy, as a concept, is simple enough to understand from the words alone. It's the amount of energy available to do stuff. The reason why we need this concept is a more difficult issue, and is directly related to the second law of thermodynamics. However, the concept itself can be understood in stating that there is some quantity we call energy, and of this quantity we can not use all of it because of the second law. That quantity which can be used in a process, however, is called Free Energy.

I skip around the second law because I myself found it hard to understand, there are several ways of explaining it, and with reference to chemical thermodynamics I don't know which is the best way to go about explaining it. In fact, I think it unnecessary to understand the second law when first approaching chemical phenomena so long as we conceive that there is this concept that limits the amount of energy that can be obtained from any process, and that concept is the second law of thermodynamics.

The way in which Free Energy applies to equilibrium is through a relation (or equation, expression, what-have-you) of a certain type of Free Energy, that is conveniently defined for standard laboratory conditions. This type of free energy is called "Gibbs Free Energy", because it was invented by Josiah Willard Gibbs. This is the energy available to do work when the system is under constant pressure (or nearly so), such as you find in a laboratory at a given height above the earth. In a chemical reaction taking place in a beaker, the change in free energy can be measured with a simple thermometer. Further, the change in free energy is directly related to the equilibrium constant at a given temperature through:

ΔG = -RT ln (K)

One thing you can notice from this relationship is that if the change in free energy is positive, then raising e to the power of a negative number will give you a number less than one. Similarly, raising e the power of a positive number will give you a number greater than one. This indicates that negative changes in Gibbs Free Energy are indicative of chemical reactions where products are favored more than reactions. The converse of this is also true: Positive changes in Gibbs Free Energy are indicative of chemical reactions that favor reactants.

Naturally, one needs to know how one measures Gibbs Free Energy. The above equation is not what one would call the definition of Gibbs, or give someone a good way of measuring the change in Gibbs free energy, but only its relation to the equilibrium constant. However, I think I'll save that discussion for later. Currently what is more important to grasp is that Free Energy and equilibrium and linked together, and that Free Energy is a thermodynamic concept which is why questions of equilibrium and answered through the concepts of thermodynamics. However, in first understanding chemical reactions, one need not have the grounding principles of thermodynamics down: One need only understand equilibrium as a ratio of products of reactants in a chemical reaction, and that this ratio of equilibrium is governed by the concept of available free energy in a chemical system. That, I think, is the basic beginning to understanding the thermodynamics of chemistry without basing that understanding in the thermodynamics proper.

Equilibrium as a General Model

I think I'm going to have a series of posts on the basics of thermodynamics and its application to chemistry because, well, it's so darn interesting.

In the previous post I outlined some basic concepts of chemical equilibrium. But the case that I gave was very specific and would only apply to a system that operates in a similar manner -- namely, that one molecule of X would combine with one molecule of Y to form one molecule of XY. This is not always the case. But before going into specific chemical equilibrium, I think it better to look at where the model for equilibrium comes from.

A model for physical systems can be constructed from the concept of a system and surroundings. Both are selected by the modeler, usually specifically selected for convenience of calculation, and in that sense are arbitrary. The system is simply what you are interested in. The surroundings includes everything else, but usually only the immediate surroundings are all that are taken into account -- a chemical example would be what is in a beaker for a system, and the lab that the beaker is in for the surroundings.

In designating a system/surroundings, you have some quantities that can describe both: Energy, Pressure, Temperature, Volume, and moles of gas. Any of these quantities can be exchanged between the system and the surroundings, and which quantities can be exchanged often describe the type of system that you are looking at.

A common example from physics is the mechanical equilibrium of a spring represented by the following force diagram.
(Do forgive my Paint abilities). According to Newton's Second Law

ΣF = Fs + Fg
Fs = -kx
Fg = mg
And, because this system is in equilibrium ΣF = 0
Therefore, Fs + Fg = 0, and Fs = -Fg, which means by substitution kx = mg

Which happens to usually be a highly convenient situation. In particular, note that the previous solution had no reference to time. This is something unique to equilibrium solutions: There is no reference to time, only to what each respective variable is at when no variable of interest is changing.

However, when dealing with the system/surroundings model, usually forces aren't the variables of interest. A close analogue. A common example of pressure equilibrium would be a balloon which has been tied off. The gas within the balloon would have a higher pressure than the exterior pressure, but pressure would not be exchanged between the system (the gas in the balloon) and the surroundings (the room the balloon is in).

This situation can occur between any variables of interest -- Pressure, Volume, Temperature, Energy, and chemical concentration. The final one is the one that chemists are first introduced to. This is, ultimately, just the application of thermodynamics/statistical mechanics to chemical systems. Ergo, the study of the model of equilibrium is actually the study of thermodynamics, which is one of the main branches of chemistry. The above explication of equilibrium should also clarify why it is that kinetics, despite being related to energy just as thermodynamics is related to energy, is a separate case of study: The concept of equilibrium requires things to not change with time, and the concept of equilibrium is the model within thermodynamics most often used to model chemical systems as, regardless of the time it takes, the system will tend towards concentrations which satisfy the equilibrium constant.

I think this is done mostly to simplify predictions: thermodynamics, I must admit, is still a bit of an impenetrable thick fog as it is. Not having to worry about time-dependence makes things a little easier.

Equilibrium, Basic Chemical Approach

In a previous post I mentioned that there are two things one must consider in analyzing a chemical reaction: thermodynamics and kinetics. The model of equilibrium covers the first of these.


Equilibrium, in its most basic sense, is the ratio between what is created in a chemical reaction and what was used in a chemical reaction. Suppose the following general chemical reaction:

This reads as "Chemical X and Chemical Y react to yield Chemical XY in equilibrium" Many chemical reactions will include a simpler notation for their "react to yield" symbol such as "→" because most reactions that one is introduced to in a general chemistry course fully react to products. The vast majority of chemical reactions do not have this feature, however, and the double arrow symbol above is used to indicate that both products and reactants are being formed when the system has reached chemical equilibrium.

However, the relative amounts of product and reactant can be predicted through the use of an equilibrium constant. Each chemical system has its own equilibrium constant, but the equilibrium constant remains the same for systems prepared with the same chemicals and under the same surrounding conditions. This constant can be found from the following:

This states that the concentration of chemical XY divided by the product of the concentrations of chemical X and Y equals a constant -- specifically, the equilibrium constant. This means that given a certain reaction and its equilibrium constant, one should be able to predict the concentrations each species will have when equilibrium is reached -- and you can do so. This is a very tidy result because chemists have to model ~10^23 particles all interacting at once. This allows one to predict effects in the physical world while ignoring things such as electric fields, momentum, and position. For example, if one has the equilibrium constant one can be a qualitative prediction about the relative concentrations of products to reactants. If the equilibrium constant is greater than one, then products are highly favored. This is the case with many introductory chemical systems one studies, which is when the symbol → is used since products are so highly favored. However, if the equilibrium constant is smaller than one, then reactants are more favored than products in this particular chemical reaction.

This equilibrium relationship governs the reverse reaction as well: if one where to look at the reaction , then the equilibrium constant for this reaction would be the reciprocal of the previous reaction. This is easily proven if you simply place the concentration of the products of this reaction multiplied together over the concentration of the reactant.


Of course, it also has its own set of limitations. The equilibrium constant is only constant for a given temperature. It can also be somewhat difficult to actually obtain the equilibrium constant, though there are several methods of doing so. Further, as I've previously mentioned, the equilibrium constant says nothing about the kinetics of the reaction: Only the relative energy of the products and reactants, or how favorable the reaction is thermodynamically. This can be important in synthesizing chemicals as two different products could be likely to form, but because of one product is slow to form, the other product is the major chemical created.

Choosing a Method

Every field has a methodology. Adhering to a methodology may seem the best way of retaining objectivity, but last night I found experienced methodologies, arriving at valid conclusions within the reference frame of their method, that conflicted. This was the result of a philosophical discussion after watching a debate on whether or not the resurrection of Jesus is true. Now, the conflict is not irreconcilable on either side -- both sides could explain the other in their own terms -- so there wasn't a want of consistency on either party. But there was a lack of a definitive answer, as is often the case in philosophical questions.

Though this is not, by necessity, a philosophical question. The answer can require a philosophical method, but it does not necessitate it. The Pro side used a historical method. I can't meaningfully comment on the historical method, but I can say that it seeemed the Pro side should be treated as an expert. The argument, to my philosophical knowledge, was valid. The case that his argument failed, and I knew that it failed, was in my knowledge of the scientific method. Resurrection, to the best of our knowledge, is highly unlikely to be possible. The best inference, at this point, is to conclude that Resurrection can not happen. Naturally this doesn't mean that it can't happen. But I would also point out that nothing has brought us closer to knowledge than the method of science. However, in the case of historical details, that remains problematic -- thereby the need for a historical method.

I would place the scientific method above the historical method in its ability to ascertain the truth due to my experience with the method. But, supposing that your world-view allowed resurrection, and you apply the historical method, everything seemed to fall well into place. So, in some sense, the debate becomes an argument of metaphysics -- hardly the appropriate place for truth-determination.

So, in what way does one choose a method? The whole point of creating method is to become as objective as possible. Yet there is a multiplicity of methods. While, normally, the choice of method is obvious (Are you investigating the world? (science) Are you investigating the past? (history) Are you investigating wisdom? (philosophy).), there can come a point where two individuals can come to an impasse on some questions, such as the resurrection example, and both think their method is the most objective way to truth, yet come to different conclusions. I believe that both debaters were making good-faith efforts for their position, as opposed to playing polemics to "win", so I don't think an ego-driven hypothesis resolves the question. Surely anyone interested in proper conclusions can admit that they don't want the ranking of methods to be dictated by how comforting we find their conclusions, or how well they justify everything we already believe -- that would entirely defeat the point of method! 

How do you rank methods, and why?

The Scientist and Society

I have politics on the brain, with the state of the union address coming up, and as such have been lead back to what Cassidy's "Uncertainty" started: The interplay between science, scientists, and politics.

On the face of things it seems that the best a scientific minded individual to do is affect apolitical attitudes. This is what scientific organizations tend towards, and I think it's a good thing. We want our society to make decisions based upon the world we live in, so the best way to have this political influence is to not discuss or make statements about standard political questions. In some sense this is problematic, as we currently see debates on religion in public education, or we have a single political party that primarily speaks against global warming, but in these cases there are firm scientific reasons for taking a position: 1) Religion ain't science. 2) Data and the mainstream interpretation of that Data. In short, the success of the scientific method.

I can't agree more than with this position for scientific societies. It is in this way that they can best help society, in general. However, I wonder if this attitude is best for the scientific individual. Given I live in the United States, I would infer that the usual reply would be "No. The individual can express whatever they wish, so long as they, personally, take credit for said comment, and do not speak in the name of X organization". But, as it is in this way that scientific communities can better help direct their communities, if said individual is attached to such-and-such a cause in popular culture, it could put political question on any scientific pronouncement said individual has. In conflict with this is the premise that, as individuals, we ought to have the freedom to express our political affiliations outside of any other affiliations that we may harbor. However, people don't operate in said manner. They can attempt to separate the individual from their various affiliations, and even make a good faith effort to do so -- but we still retain knowledge of an individuals full social affiliations. And if we do, indeed, wish to effect society in the most positive way that a scientist can, it may be the case that we ought to forgo public political opinions in favor of public scientific pronouncements.

I don't pretend to have an answer to the question, I am only raising it as a question to be thought and ranted about. The converse of this position is, of course, the life of Werner Heisenberg. He's an extreme case, however, and we do not currently live in quite as extreme a time as he did, so I do not think his life example is a good example to base current opinions off of. However, I think most will agree that his example definitively states that there is, in the case where one accepts keeping quiet about political opinions, a point (line, plane?) somewhere when that person should stop playing the apolitic become publicly political. But under what circumstances is that the case, and can one even determine those circumstances during the times that those circumstances exist?

I wish there was a journal or forum for ethical discussions amongst the scientific community -- though that may violate the "Objective"-ness of the scientist on the political landscape.

K-INBRE Symposium

I just got back from a weekend conference hosting individuals to present their research in speech format. I've gone to one symposium before, but in this one I actually had a poster to present. And... it was not anywhere near as bad as I had thought it would be. I used to do performance art, so perhaps I shouldn't have been nervous, but the subject matter was different. In performance art you have a role to play, to entertain people. With a poster... I thought it would be different. But then I ended up just telling jokes and playing the role of "elucidator of research" -- sort of in the same fashion that I try and tutor people. All of the people who looked at the poster probably had a better knowledge of biochemistry than I, as I've just been learning biochemical terms specifically related to my organism and I'm a chemistry undergraduate who has yet to take biochem, but everyone seemed pretty generous and forgiving. If they asked a specific question, sometimes I would and sometimes I would not know, and I would be blunt and let them know if it were the case that I was ignorant. They nodded and let me finish the "shpiel" I prepared in explaining the poster, and some of them even taught me things. It was a very positive experience, and hopefully next year I'll have a better working knowledge of biochem and, please oh please may this year yield presentable results. 

Significant Figures

Oi! Well, the winter break is over (which is my excuse for Winter mute-ness), and I've hit the ground running again. As the Cake is a Lie, Syllabus Day is a myth.

Today I heard the best formulation for what significant figures are:

The mathematical method for keeping track of the least accurate measurement.

From this least accurate measurement in a series of measurements, you can tell just how well you know the "true" value of a given measurement. I don't know if this just went over my head in early chemistry classes, but I'll remember it now because it solidified all the abstruse rules I've been utilizing to no purpose aside from it being something... necessary... because, like, yeah...

It's not as if the rules are terribly difficult, unto themselves, but I don't recall ever knowing why I was using them. Obviously they were significant (harhar), but to what end... eh. However, this helps me understand why the addition of significant figures only depends upon the number with the least decimal places. If you add what you measure to be 2.5 Liters to a measured .0532 Liters, the relatively large uncertainty in the first measurement will "wash out" the relatively finer accuracy in the second measurement, giving you "'bout 2.6 Liters".

This leads perfectly into Uncertainty in measurements, which is related but something we utilize in the more formal sense in our everyday life. If you're getting off the clock in 16.3 minutes, you'll likely think of it as "15 minutes". And, for the purposes at hand (having a feeling for when you're going to get off), that level of accuracy is perfectly acceptable. If, then, someone asks you to stay for 5, you'll probably realize they don't mean "5.00 minutes", but rather there is some variance (or whatever it might mean in your particular social context). This is us utilizing the uncertainty in their measurement (their feeling for how long it will take until an extra task is done) that can be modeled mathematically: This could take plus or minus such-and-such an amount of time. "5 minutes" doesn't mean " 5.00 minutes", but maybe 5.0 plus or minus .5 minutes (or whatever). While you know from the clock that you have 16.3 minutes, the most number of significant figures you can keep is determined by their measurement of 5.0 minutes plus or minus .5 minutes, so you add the two measurements together and obtain that you could be on the clock from 21 minutes to 22 minutes after rounding off with significant figures. Perhaps a better model of conversation and on the fly estimates would actually use 5 plus or minus 4 minutes. From this you could conclude that you could be on the clock between 20 to 30 minutes, because then you would only have 1 significant figure. I mean, sure we don't actually go through the step-by-step analysis, but we tend to have a "feeling" for these things in conversation despite not knowing how we can conclude that our "feeling" may or may not be correct. I think the above expressed well what I always intuited about significant figures but never concretely expressed.